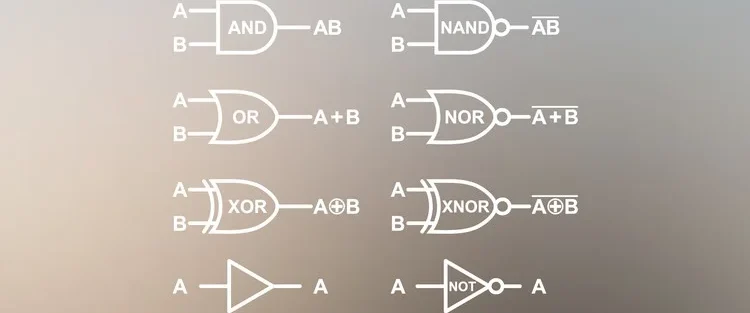
This is a Computer Maths Assignment Help Example focusing on Boolean Algebra, Logic Gates, and Logic Circuits. The assignment covers the simplification of complex Boolean expressions into minimal forms, truth table construction, and the evaluation of logic circuits. It provides a step-by-step guide to solving problems in Boolean logic for students in computer science and mathematics.
Discrete Mathematics is considered an important subject in Computer Studies, and this includes solving complex boolean expressions. The following sample work on Computer Science Maths will not only help students understand how to solve Discrete Maths and Boolean Algebra questions but will also help them understand the high-quality assignment help we deliver to our beloved students.
Note:
If you need Computer Science Assignment Help, Click here.
If you need Maths Assignment Help, Click here.
Discrete Mathematics Assignment Help for Computer Science Students on Boolean Algebra
Assignment Question: Simplify the given Boolean expressions into minimal forms using truth tables and logic gates. Evaluate the corresponding logic circuits for accuracy and efficiency.
Type: Computer Science Assignment Help
Sub-type: Computer Science Mathematics
Level: Bachelors Studies
DISCRETE MATHEMATICS II FOR COMPUTER STUDIES
Resources: Laws of Boolean Algebra
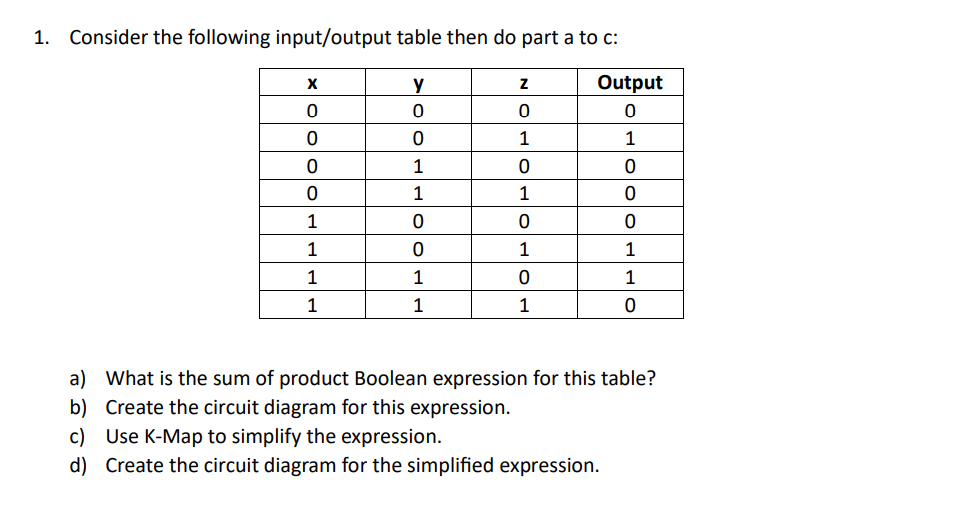
Question 1:
You may also like checking Final Project Ideas for Computer Science and Engineering Students
Solution 1:
a)
X | Y | Z | OUTPUT |
0 | 0 | 1 | 1 |
1 | 0 | 1 | 1 |
1 | 1 | 0 | 1 |
Output = (~x ∧ ~y ∧ z) ∨ (x ∧ ~y ∧ z) ∨ (x ∧ y ∧ ~z)
b)
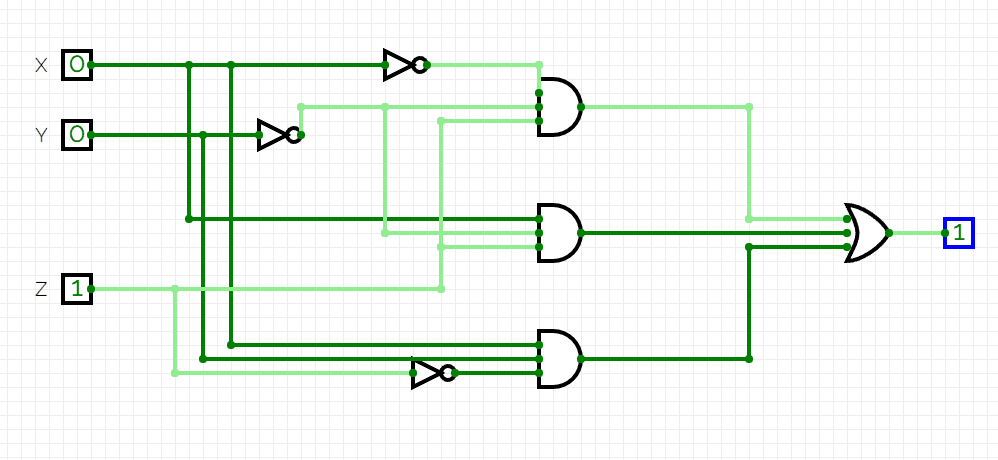
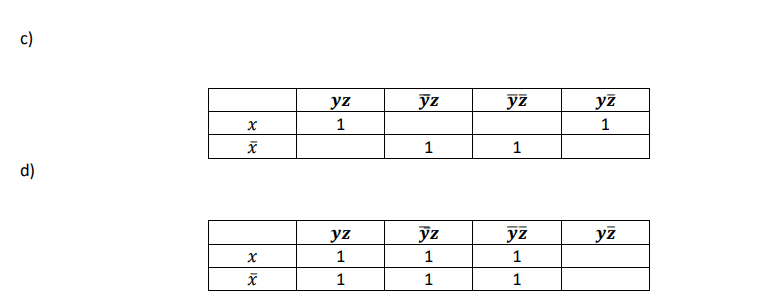
c)
~Z | Z | |
~X~Y | 0 | 1 |
~XY | 0 | 0 |
XY | 1 | 0 |
XY | 0 | 1 |
Simplified Expression: xy~z + ~yz
d)
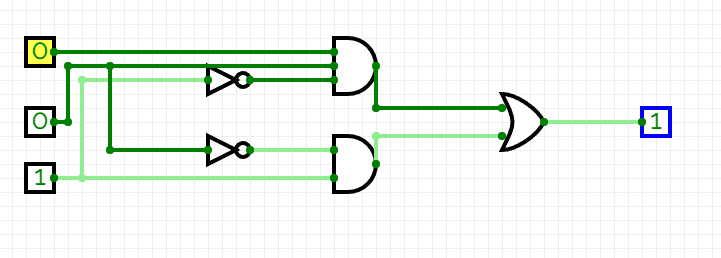
Question 2:

Solution 2:
a)
A | B | C | ~A | ~B | ~A+~B+C |
0 | 0 | 0 | 1 | 1 | 1 |
0 | 0 | 1 | 1 | 1 | 1 |
0 | 1 | 0 | 1 | 0 | 1 |
0 | 1 | 1 | 1 | 0 | 1 |
1 | 0 | 0 | 0 | 1 | 1 |
1 | 0 | 1 | 0 | 1 | 1 |
1 | 1 | 0 | 0 | 0 | 0 |
1 | 1 | 1 | 0 | 0 | 1 |
b)
A | B | C | AC | ~A | B+ AC +~A | A(B+ AC+ ~A) |
0 | 0 | 0 | 0 | 1 | 1 | 0 |
0 | 0 | 1 | 0 | 1 | 1 | 0 |
0 | 1 | 0 | 0 | 1 | 1 | 0 |
0 | 1 | 1 | 0 | 1 | 1 | 0 |
1 | 0 | 0 | 0 | 0 | 0 | 0 |
1 | 0 | 1 | 1 | 0 | 1 | 1 |
1 | 1 | 0 | 0 | 0 | 1 | 1 |
1 | 1 | 1 | 1 | 0 | 1 | 1 |
Question 3:
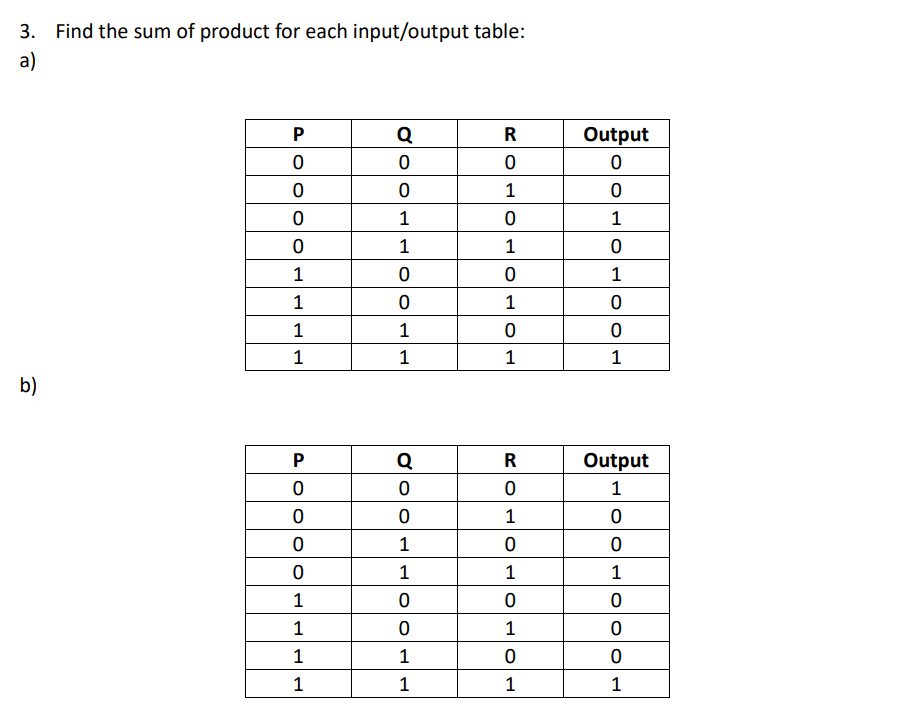
Solution 3:
a)
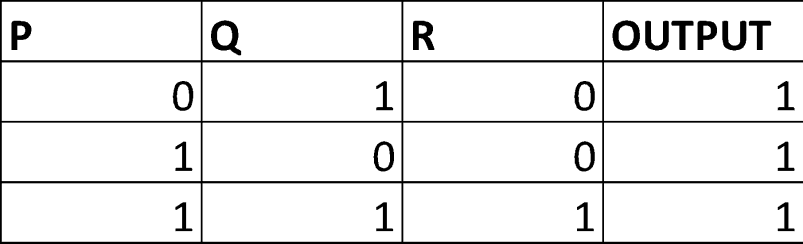
Output = (~P∧Q∧R) ∨ (P∧~Q∧~R) ∨ (P∧Q∧R)
b)
P | Q | R | OUTPUT |
0 | 0 | 0 | 1 |
0 | 1 | 1 | 1 |
1 | 1 | 1 | 1 |
Output = (~P∧~Q∧~R) ∨ (~P∧Q∧R) ∨ (P∧Q∧R)
Need help with Boolean Algebra assignments? Contact us for expert guidance!
Question 4:

Solution 4:
a)
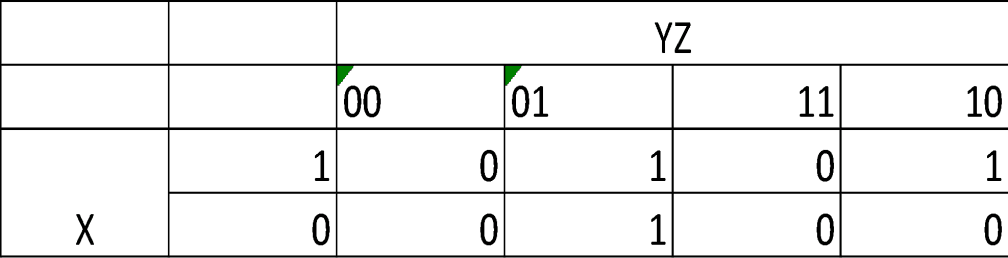
Output = (~X) ∨ (X∧Y∧~Z) ∨ (X∧Y∧~Z)
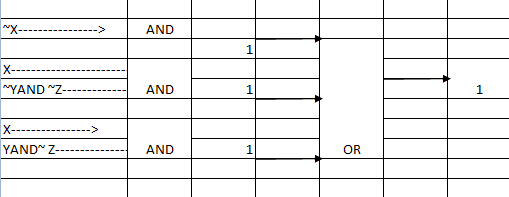
b)
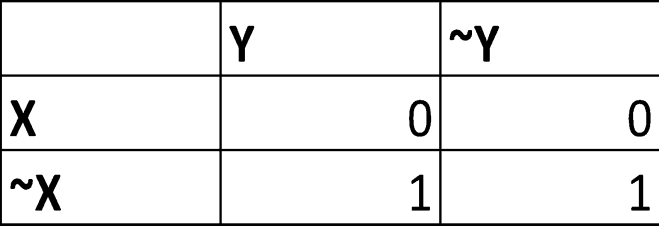
Output = ~X
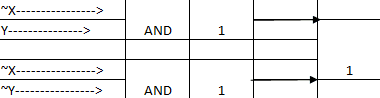
c)
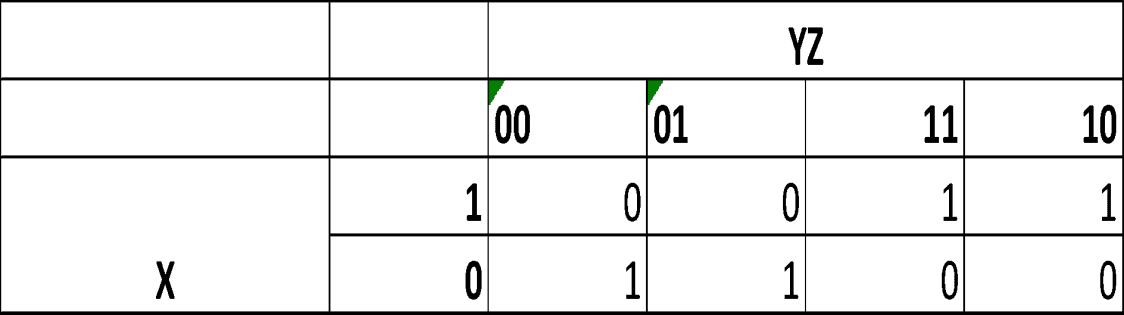
Output = (~Y) ∨ (X)

d)

Output = (U) ∧ (Y∧~Z)
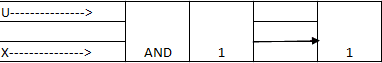
Question 5:
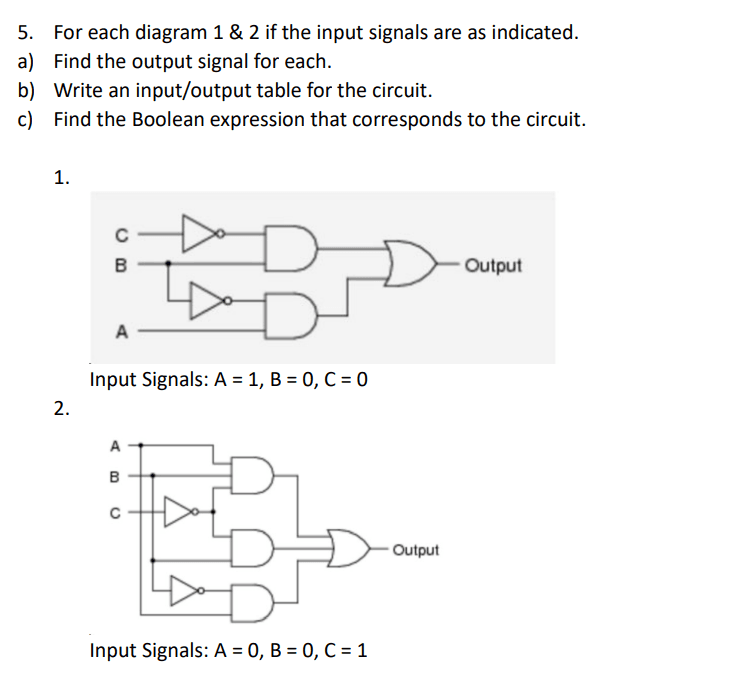
Solution 5:
This explanation addresses the functionality of two logic circuits and their corresponding outputs, input/output tables, and Boolean expressions.
1a) OUTPUT:
Inputs: A = 1, B = 0, C = 0
Output: 1
Explanation:
Follow the path from input C (0) to the bottom in put (0) of the topmost AND gate. Since C is 0, ~C will be 1. So the output of the topmost AND gate is AND (0,1) = 0. The bottom AND gate has inputs ~B(1) and A(1) which results in AND output of 1. Therefore, the OR gate inputs are 0 and 1. OR of 0 and 1 is 1. Thus our output is 1.
1b) INPUT/OUTPUT Table:
A | B | C | Output |
0 | 0 | 0 | 0 |
0 | 0 | 1 | 0 |
0 | 1 | 0 | 1 |
0 | 1 | 1 | 0 |
1 | 0 | 0 | 1 |
1 | 0 | 1 | 1 |
1 | 1 | 0 | 1 |
1 | 1 | 1 | 0 |
1c) Finding the Boolean expression that corresponds to the circuit:
Disjunctive normal form = ~ab~c + a~b~c + a~bc + ab~c
Minimal Form = b~c + a~b
2a) OUTPUT:
Inputs: A = 0, B = 0, C = 1
Output: 0
Explanation:
A is 0, so topmost AND gate output will be 0. B is 0, so middle AND gate output will be 0.
Similarly A(1) is an input to the most bottom AND gate. So output of the most bottom AND gate is 0.
Therefore, input for OR gate is 0,0,0 which results in OR output of 0.
2b) INPUT/OUTPUT Table:
A | B | C | Output |
0 | 0 | 0 | 0 |
0 | 0 | 1 | 0 |
0 | 1 | 0 | 1 |
0 | 1 | 1 | 0 |
1 | 0 | 0 | 1 |
1 | 0 | 1 | 1 |
1 | 1 | 0 | 1 |
1 | 1 | 1 | 0 |
2c) Finding the Boolean expression that corresponds to the circuit:
Disjunctive normal form = ~ab~c + a~b~c + a~bc + ab~c
Minimal Form = b~c + a~b
To understand more about Boolean Laws, check this article.
Also Read: